desktop version

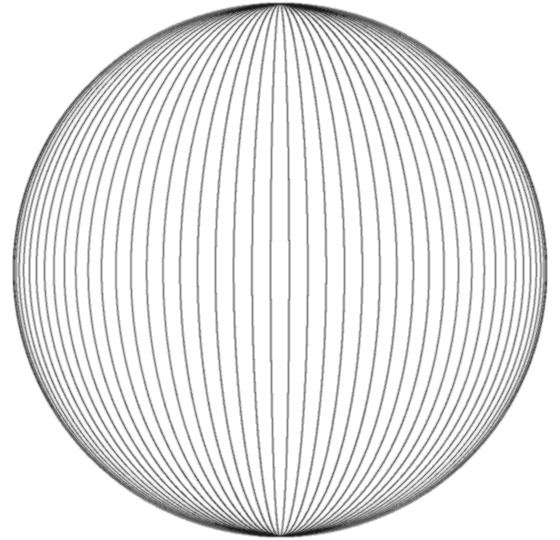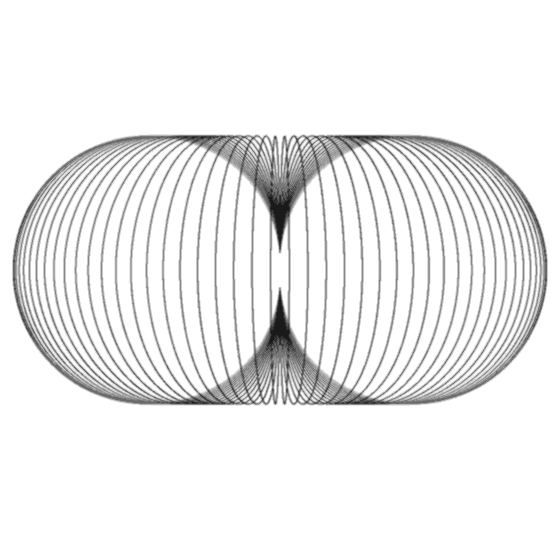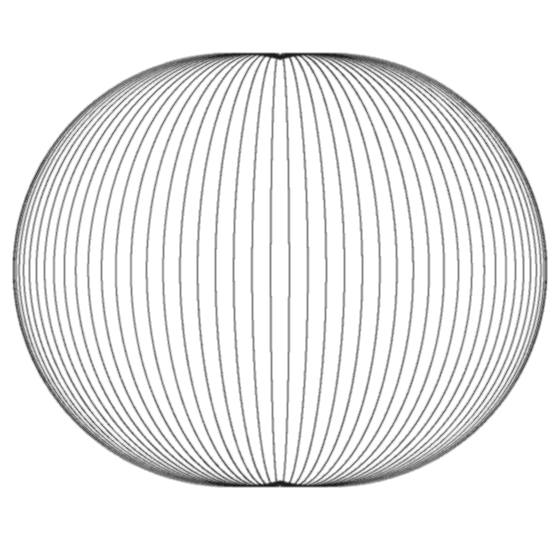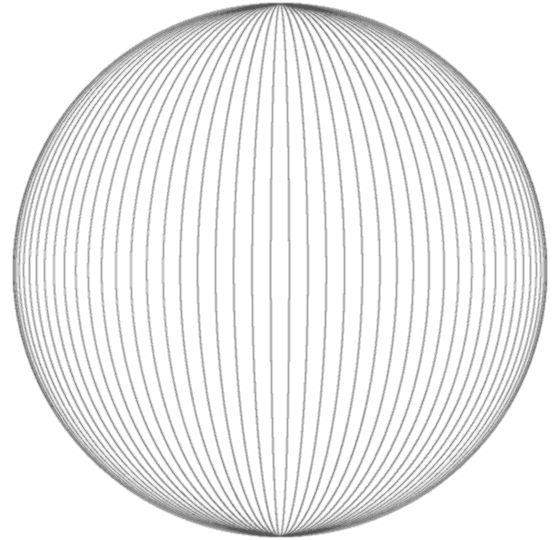
If you consider the originating sphere as Riemannian, then the two points which represent zero and infinity are identical after transformation to the horn torus! That causes a strange, nearly contradictory topology: the horn torus appears as a simply connected clopen set* and as differentiable manifold with Riemannian metric, though the topological properties have to be reviewed (until now science ignored the horn torus completely),
 
as example we introduce a bijective conformal mapping / conventional method of constructing the horn torus
 
*) consider that a line surrounding the horn torus bulge only once (e.g. a longitude) is not a closed curve, it corresponds to a line with zero as boundary point, but when circling around twice or more, it is closed without border. This fact will become important later when identifying closed lines on the horn torus surface through the center ('resonances', Lissajous figures) as figurative analogues to elementary particles ...
 
clopen: closed and/or open, depending on interpretation of neighbourhoods of point S (disjoint or connected) ...
 
topology gets totally intricate when we incorporate inverse figures (as solids and as numbers) into our reflections (nice ambiguity!), e.g. by simply interchanging longitudes and latitudes. In the dynamic horn torus model we then change from an infinite number of particles within one universe to an infinite number of universes within one particle or 'entity', but that's another, exciting story ...
 
mathematicians, physicists, join in! the horn torus is worth and necessary to be treated scientifically: the horn torus is an excellent graphical representation of complex numbers, a compactification with considerable more properties than the Riemann sphere has, it connects zero and infinity in an amazing way, can be dynamised by two independent turns, rotation around the axis and revolution around the torus bulge, what creates an incredible complexity and forms a coherent comprehensive entity, also explaining the potential for self-interaction and fractal order of complex numbers, and finally - most important - horn tori can be interlaced into one another and so very well symbolise correlation between entities, easily interpretable as physical objects: 'space', 'time', 'particles', 'forces' ...
 
... and considered more generally: classical mathematics* does not offer any well-elaborated and consistent theory of topological systems ('spaces') that are based on (respectively 'spanned' by) continuously and dynamically changing coordinates. Most practically working physicists doesn't bother that too much. They may be happy and content with their sophisticated software for computer simulations, animations and evaluations as explaining models for dynamic processes, being very successful thereby - no doubt, but from a more philosophical point of view that's not exactly the ideal solution for describing a dynamic physics. For true understanding we are in urgent need of revolutions (in thinking and as 'turns' :-), we should reflect on the topic more constructively, starting from a very basic level after having achieved full abstraction from our traditional imagination of (more or less static) spaces with embedded objects and processes by strict epistemological reduction to fundamental entities, and we have to aim at a - maybe disruptive - congruent mathematical model of physical 'reality' that comprises the pervasive and unstoppable dynamic as main intrinsic property. - Static doesn't occur in quantum reality, and no model works sufficiently without underlying dynamic. That's for sure! 
 
→ texts  /  video  /  start page  /  desktop version  /  artmetic
 

 
* With the horn torus model we leave 'classical mathematics'. Though we pragmatically make use of well established skills in three dimensions to illustrate the dynamic, the model is not dimensional - neither Euclidean nor non-Euclidean, neither related to any vector space nor even connected to Hilbert spaces and the respective formalism - at least not in an obviously predominant way. Horn tori, in particular the 'small' ones, induce an extremely dynamic and complex geometry and simultaneously - the 'big' ones - are capable to form a nearly static 'flat space' with Euclidean rules when approaching 'infinite size'. Conventional methods are insufficient or too laborious to describe such a hybrid of dynamic and static space properly and we maybe have to await further progress in quantum computing for an appropriate approach and adequate treatment. Then mathematics surely will experience changes, and surprises in physics cannot be ruled out. But note: here and now, on these pages, we only play a preliminary game!
 

 
As addition concerning topological questions here an excerpt from my paper
The horn torus model in light and context of division by zero calculus  (2021):
 
 
It is easily detectable that the 'north pole' N of the Riemannian sphere, which represents infinity, and point 0 (zero) combine in the centre of the original sphere to one single point S after the described transformation to a horn torus, where all longitudes (meridians) of the horn torus touch the symmetry axis through N and 0.
 
The topology of this figure is very intricate: during transformation the sphere loses its compact property, because N and 0 only remain on one single half longitude each during bending. Compactification then is re-established, as soon as N and 0 combine to one single point (S), but now one of the points has disappeared. Perhaps it makes more sense to revoke the Alexandroff compactification first, what means, point N has to be removed before transformation, and we regain the compactification with point 0 alone. Infinity then is replaced by Zero! This notation seems to be a very helpful aspect in the division by zero calculus.
 
The topology however has to be reviewed thoroughly. We are confronted with a strange, nearly contradictory topology: the horn torus appears as a simply connected ‘clopen’ set and as differentiable manifold with Riemannian metric, but that occasionally is discussed rather controversially: how are the neighbourhoods of point S interpreted? are they disjoint or connected? is the horn torus an open set? or closed, maybe? clopen, as indicated? is it connected at all? simply connected then? or multiply connected?
 
Even for the static figure there is no clear consensus, and for the dynamized horn torus then, where rotations around the axis and revolutions around the bulge occur, the situation gets totally intricate and weird. As an example of weirdness, consider that a line which surrounds the horn torus bulge only once (a longitude e.g.) is not a closed curve, it corresponds to a line on the Gaussian plane, with zero as boundary point, but when circling around twice or more (an even number times!), it is closed without border and can be contracted to a point, however, a certain problem with compactification remains, because lines lack one point, either on the north or on the zero side, again depending on interpretation of point S and its neighbourhood.
 
All our considerations about topology of the horn torus so far are restricted to the static figure. The properly meaning of the horn torus model with physical interpretations however will be completely different, and the static topological results have no relevance for the dynamic properties there. All lines which appear on the horn torus surface, likewise are dynamical and, as such, they pass point S from ‘zero’ to ‘infinity’ and vice versa equicontinuously.
 
Topology gets maximally intricate when we incorporate inverse figures (as solids and as numbers) into our reflections (nice ambiguity!), e.g. by simply interchanging longitudes and latitudes. In the dynamic horn torus model we then change from an infinite number of particles within one universe to an infinite number of universes within one particle or ‘entity’, but that's another, exciting story ...