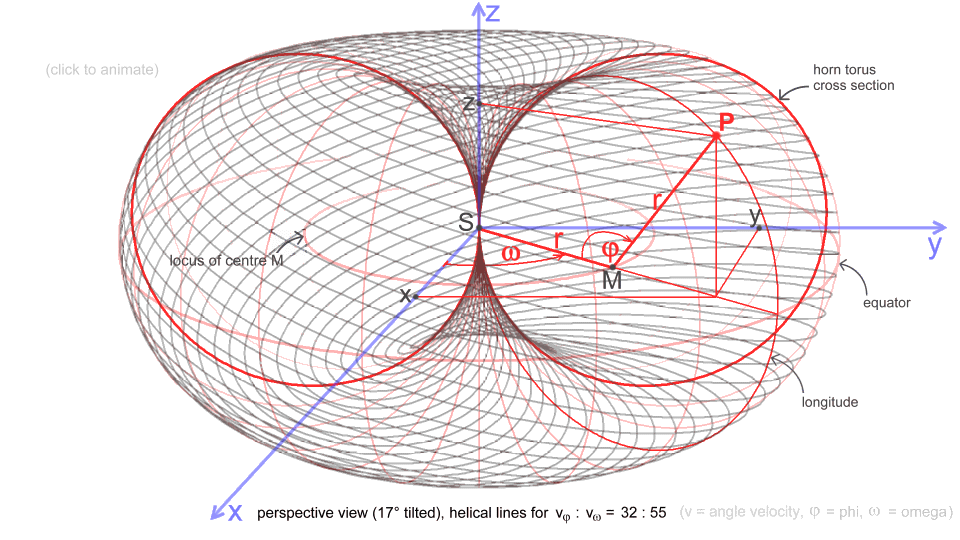
coordinates for this animation and its parametric form (source) :
for all points P on the surface of a horn torus with fixed radius r is valid
x = r·(1 − cosφ)·cosω
y = r·(1 − cosφ)·sinω
z = r·sinφ
the 'unrolling line', indicated in the animation, is divided into two parts
(referring to the standard dynamic horn torus as unit): r > 1 and r < 1
case r > 1: r and ω increase with φ, starting with φ1 = 2π, according
r = φ / 2π (↝ r1 = 1) and ω = r·φ = φ2 / 2π (↝ ω1 = 2π), so we have
x = (1 − cosφ)·cos(φ2/2π)·φ/2π
y = (1 − cosφ) · sin(φ2/2π)·φ/2π
z = sinφ · φ/2π