|
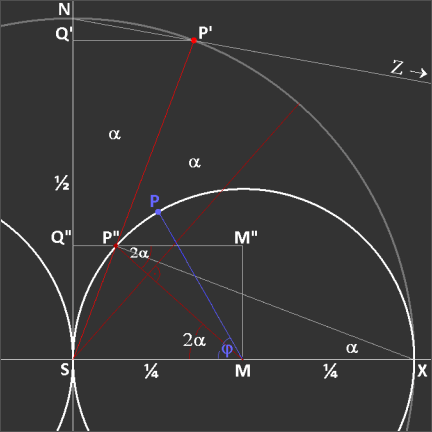
→ front page / sitemap / previous page (rectangular mapping) Search for conformal mapping from Riemann sphere to horn torus and directly from complex plane to horn torus (considerations are not associated with the dynamic model) Bend a half longitude continuously to a circle, preserving its length, as shown in the figure below for two opposite ones (treat all half longitudes in this manner simultaneously and recognize that they pass through a series of different spindle tori). The finally obtained cross section of the horn torus bulge has doubled the original angles (from π to 2π), so conclude (fig. 2): to project a point P' from the Riemann sphere onto the horn torus first double the angle α between closer pole (here N) and the point's radius, then draw the perpendicular line from the horn torus bulge (!) center M to this leg of the doubled angle and intersect with horn torus (choose the intersection P" on the same 'hemisphere' on which the original point P' is located on the Riemann sphere). It is the same point as the intersection with the original radius! That was submitted by Vyacheslav Puha already. Now consider and compare the lengths of corresponding latitudes on Riemann sphere and on horn torus (see below): on sphere we have |
click animation to stop  |
 |
SN = 1/2 (N is 'north pole', S is center, not south pole) P'Q' = 1/2 · sin(α) P"M" = 1/4 · cos(2α) P"Q" = 1/4 · (1 - cos(2α)) length of latitude through P': 2π · P'Q' = π · sin(α) length of latitude through P": 2π · P"Q" = π/2 · (1 - cos(2α)) = π · sin2(α) Z is the intersection of the stereographic projection line from north pole N through point P' with the complex plane, tangent in south pole 0 of Riemann sphere For compilation we better choose the version with α = 0 at south pole: continue ⇒⇒ |