conformal mapping sphere ↔ horn torus
Due to the hope that a geometrical solution for the conformal mapping between sphere and horn torus could be found, analogue to the Riemannian stereographic projection, it first seemed necessary to nest horn torus and sphere into one another, resulting in a bit confusing drawings and derivation. But until now the search came to no result (Vyacheslav Puha's ingenious method unfortunately is not conformal, and probably no geometrical method does exist), and so we study sphere and horn torus separately. We don't declare any appropriate stereographic projection and try to proof afterwards the conformality but we use instead the conditions of conformality to compile and establish the wanted mapping analytically:One condition for conformal mapping is that small circles on the origin are mapped as small circles on the target surface and therefore we want to construct small circles on both surfaces that only are dependent on the position of points P on the surface, i. e. only dependent on the angles α = ∠NMP for the sphere resp. φ = ∠SMP for the horn torus. Due to rotation symmetry of both figures the rotation angle ω doesn't play any role and is arbitrary, and likewise, because of mirror symmetry, α can be exchanged by π - α (what corresponds to the exchange of north and south pole of the sphere) and φ can be exchanged by 2π - φ. Even the radii r of both figures turn out to be arbitrary and independent. Following drawing shows longitudes, spacing 10°, and latitudes, spacing 20°, P located at angles α = 50° resp. φ = 140°, ω = 35° on both figures:
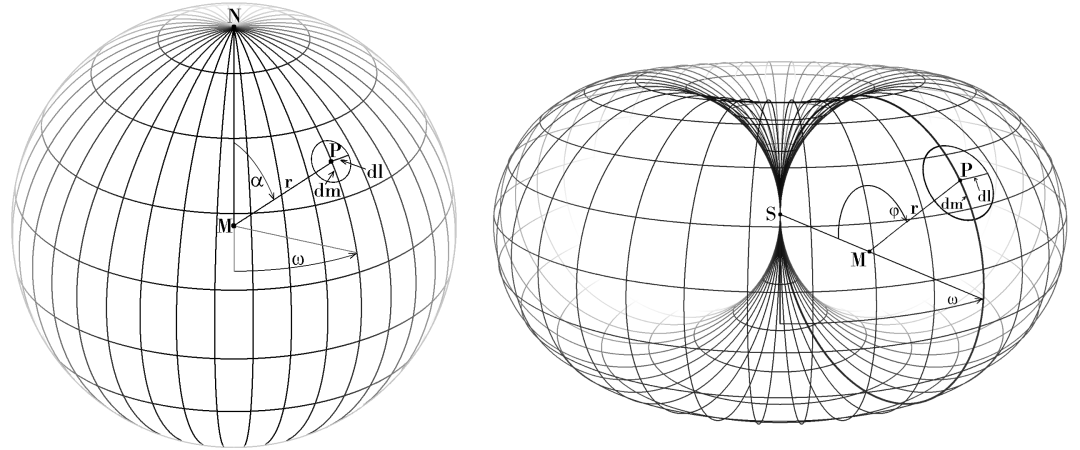
|
We consider the small circle around any point P and state the condition that the radii dm (in direction of meridians) and dl (parallel to latitudes) have to be equal. Lengths m of longitudes (meridians) on both figures, sphere and horn torus, are m = 2π·r Lengths l of latitudes are computed differently (* see supplement for derivation):l = 2π·r·sinα on the sphere and dm = r·dα on the sphere and dl = dω·r·sinα on the sphere and dα = dω·sinα for the sphere and dα/sinα = dφ/(1 - cosφ) and finally by integration we obtain the condition for conformal mapping∫(1/sinα)dα = ∫(1/(1 - cosφ))dφ horn torus → sphere: (0 < α < π, 0 < φ < 2π, C any real number) C is a kind of 'zoom/diminishing factor' for the mapped figures and shifts them:case α → φ: φ moves towards 2π with increasing C > 0, towards 0 with C < 0, case φ → α: α moves towards π with increasing C > 0, towards 0 with C < 0, conformality is given for C ≠ 0 as well, i. e. there is an infinite set of solutions - but mappings are not bijective, when C ≠ 0 is the same in the inverse mapping (likewise: Riemann stereographic projection is a special case amongst others) © 2018 Wolfgang W. Daeumler, Perouse |
* supplement: length of horn torus latitude
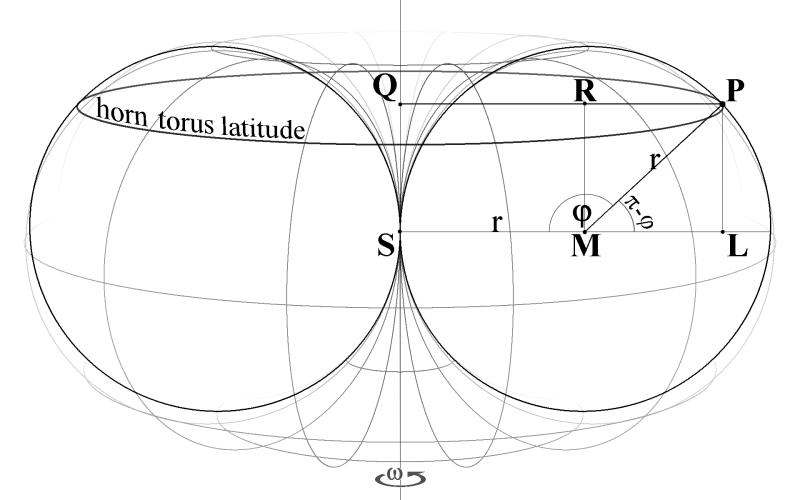
| QP = QR + RP = SM + ML = r + r·cos(π - φ) = r − r·cosφ = r·(1 − cosφ) l = 2π·QP l = 2π·r·(1 − cosφ) |
remark on the dynamic horn torus model in (quantum) physics:
the horn torus is an excellent graphical representation of complex numbers, a compactification with considerable more properties than the Riemann sphere has, it connects zero and infinity in an amazing way, can be dynamised by two independent turns, rotation around the axis and revolution around the torus bulge, what creates an incredible complexity and forms a coherent comprehensive entity, also explaining the potential for self-interaction and fractal order of complex numbers, and finally - most important - horn tori can be interlaced into one another and so very well symbolise correlation between entities, easily interpretable as physical objects: 'space', 'time', 'particles', 'forces' ...
... and considered more generally, first a word on the - strangely enough often not even realized - lack of fundamental dynamic based theories in (quantum) physics: Classical mathematics does not offer any well-elaborated and consistent theory of topological systems ('spaces') that are based on (respectively 'spanned' by) continuously and dynamically changing coordinates. Most practically working physicists doesn't bother that too much. They may be happy and content with their sophisticated software for computer simulations, animations and evaluations as explaining models for dynamic processes, being very successful thereby - no doubt, but from a more philosophical point of view that's not exactly the ideal solution for describing a dynamic physics. For true understanding we are in urgent need of revolutions (in thinking and as 'turns' :-), we should reflect on the topic more constructively, starting from a very basic level after having achieved full abstraction from our traditional imagination of (more or less static) spaces with embedded objects and processes by strict epistemological reduction to fundamental entities, and we have to aim at a - maybe disruptive - congruent mathematical model of physical 'reality' that comprises the pervasive and unstoppable dynamic as main intrinsic property.
Static doesn't occur in quantum reality, and no model works sufficiently without underlying dynamic. → continue