Horn Torus

'Geometry Of Everything'

intellectual game to reveal engrams of dimensional thinking
and proposal for a different approach to physical questions

a thought experiment as an exercise for abstraction ability
and attempt to describe 'fundamental entities' colloquially
by reducing physical laws to properties of complex numbers,
illustrated with dynamically interlaced horn torus surfaces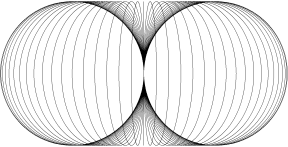

horn torus tore á trou nul Dorntorus
cross-section, longitudes spacing 5°

construction of a horn torus

2. alternate method:

take a sphere with longitudes and push in both poles
until these two points meet themselves in the center
and merge to only one residual point - our 'Point S'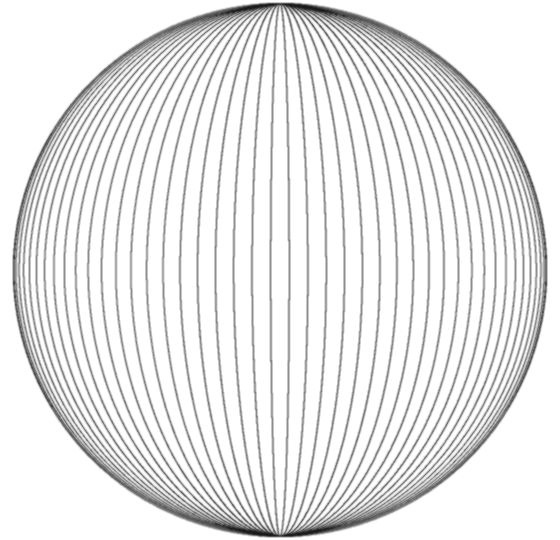
↓

↑
For mathematicians:
If you consider the originating sphere as Riemannian,
then the two points which represent zero and infinity
are identical after transformation to the horn torus!
That causes a strange, nearly contradictory topology:
the horn torus appears as simply connected clopen set*
and as differentiable manifold with Riemannian metric
though the topological properties have to be reviewed
(until now science ignored the horn torus completely)
as example we introduce a bijective conformal mapping

← conventional method / back to front page

*) consider that a line surrounding the horn torus bulge only once (e.g. a longitude) is not a closed curve, it corresponds to a line with zero as boundary point, but when circling around twice or more, it is closed without border. This fact will become important later when identifying closed lines on the horn torus surface through the center ('resonances', Lissajous figures) as figurative analogues to elementary particles ...

clopen: closed and/or open, depending on interpretation of neighbourhoods of point S (disjoint or connected) ...

topology gets totally intricate when we incorporate inverse figures (as solids and as numbers) into our reflections (nice ambiguity!), e.g. by simply interchanging longitudes and latitudes. In the dynamic horn torus model we then change from an infinite number of particles within one universe to an infinite number of universes within one particle or 'entity', but that's another story ...

mathematicians, physicists, join in! the horn torus is worth and necessary to be treated scientifically: the horn torus is an excellent graphical representation of complex numbers, a compactification with considerable more properties than the Riemann sphere has, it connects zero and infinity in an amazing way, can be dynamised by two independent turns, rotation around the axis and revolution around the torus bulge, what creates an incredible complexity and forms a coherent comprehensive entity, also explaining the potential for self-interaction and fractal order of complex numbers, and finally - most important - horn tori can be interlaced into one another and so very well symbolise correlation between entities, easily interpretable as physical objects: 'space', 'time', 'particles', 'forces' ... (→ ResearchGate Academia texts video)

as addition concerning
topological questions
an excerpt from my paper
The horn torus model in light and context of division by zero calculus
(2021)

It is easily detectable that the 'north pole' N of the Riemannian sphere, which represents infinity, and point 0 (zero) combine in the centre of the original sphere to one single point S after the described transformation to a horn torus, where all longitudes (meridians) of the horn torus touch the symmetry axis through N and 0.

The topology of this figure is very intricate: during transformation the sphere loses its compact property, because N and 0 only remain on one single half longitude each during bending. Compactification then is re-established, as soon as N and 0 combine to one single point (S), but now one of the points has disappeared. Perhaps it makes more sense to revoke the Alexandroff compactification first, what means, point N has to be removed before transformation, and we regain the compactification with point 0 alone. Infinity then is replaced by Zero! This notation seems to be a very helpful aspect in the division by zero calculus.

The topology however has to be reviewed thoroughly. We are confronted with a strange, nearly contradictory topology: the horn torus appears as a simply connected ‘clopen’ set and as differentiable manifold with Riemannian metric, but that occasionally is discussed rather controversially: how are the neighbourhoods of point S interpreted? are they disjoint or connected? is the horn torus an open set? or closed, maybe? clopen, as indicated? is it connected at all? simply connected then? or multiply connected?

Even for the static figure there is no clear consensus, and for the dynamized horn torus then, where rotations around the axis and revolutions around the bulge occur, the situation gets totally intricate and weird. As an example of weirdness, consider that a line which surrounds the horn torus bulge only once (a longitude e.g.) is not a closed curve, it corresponds to a line on the Gaussian plane, with zero as boundary point, but when circling around twice or more (an even number times!), it is closed without border and can be contracted to a point, however, a certain problem with compactification remains, because lines lack one point, either on the north or on the zero side, again depending on interpretation of point S and its neighbourhood.

All our considerations about topology of the horn torus so far are restricted to the static figure. The properly meaning of the horn torus model with physical interpretations however will be completely different, and the static topological results have no relevance for the dynamic properties there. All lines which appear on the horn torus surface, likewise are dynamical and, as such, they pass point S from ‘zero’ to ‘infinity’ and vice versa equicontinuously.

Topology gets maximally intricate when we incorporate inverse figures (as solids and as numbers) into our reflections (nice ambiguity!), e.g. by simply interchanging longitudes and latitudes. In the dynamic horn torus model we then change from an infinite number of particles within one universe to an infinite number of universes within one particle or ‘entity’, but that's another, exciting story ...