conformal mapping from complex plane → Riemann sphere → horn torus, Z →
P' → P or |z| → α → φ,
when |z| and α are zero at south pole 0 and angle φ is measured as shown in the sketch on this page,
the simpler and more consistent version (in the first considerations
I had chosen α = 0 at north pole N)
stereographic projection from complex plane to Riemann sphere, |z| → α:
α = 2·arctan(|z|)
mapping from Riemann sphere to horn torus, α → φ (C any real number*):
φ = 2·arccot(-ln(|tan(α/2)|) - C)
mapping from complex plane to horn torus, |z| → φ:
φ = 2·arccot(-ln(|z|) - C)
inverse mappings P → P' → Z, equivalent φ → α → |z|:
α = 2·arctan(e^(-cot(φ/2) + C))
|z| = tan(α/2)
|z| = e^(-cot(φ/2) + C)
derivation of formulas
(analytically by the method of infinitesimal circles) ←
excel chart for numerical computation of angles and |z|
(15 decimal places)
a graphical method (stereographic projection) Z → P probably does not exist
Vyacheslav Puha spotlights that
e lies on 'top', 1/e on 'bottom' of horn torus
but note: that's only valid for C = 0, one of infinite many conformal mappings
it's not sure whether conformality has any relevance in the horn torus model
example for a mapping that preserves right angles
between coordinates only
*) C seems to be a kind of 'zoom factor' for the mappings, diminishing
projected figures and, for C > 0, moving α and φ towards π resp. 2π,
for C < 0 towards 0 both. Likewise, but then for C > 1 resp. 0 < C < 1
(C = 1 for the stereographic projection), there exists the well known
generalised conformal mapping between complex plane and sphere![]() α = 2·arctan(C·|z|) resp.
|z| = tan(α/2) / C
α = 2·arctan(C·|z|) resp.
|z| = tan(α/2) / C
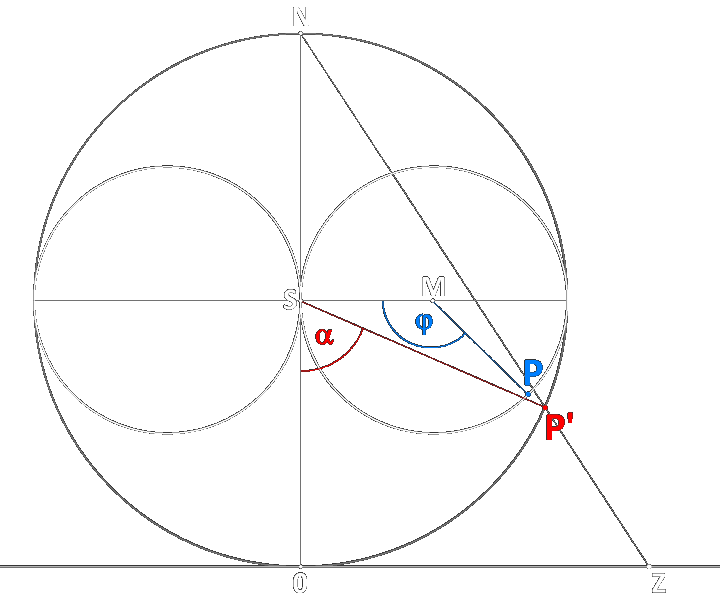
![]() Riemann sphere: 0N = 1 , ∠0NP' = α/2 ,
∠0ZN = π/2 - α/2 , |z| = 0Z
Riemann sphere: 0N = 1 , ∠0NP' = α/2 ,
∠0ZN = π/2 - α/2 , |z| = 0Z
gif
conformal mapping sphere ↔ horn torus