conformal mapping of point P' on a sphere to point P on a horn torus, equivalent to
α → φ,
when choosing α = 0 at the north pole (later
we change to version with α = 0 at south pole,
which is symmetric, but more logical and consistent, because |z| is zero here simultaneous)
![]()
φ = 2·arccot(-ln(|tan(α/2)|) - C)
![]()
we observe a small circle around P' on sphere with radius dα (α is latitude, 0 at north pole)
the radius perpendicular to screen in P' with same length is dω = dα / sin(α) (ω is longitude)
the projected small circle around P on horn torus has same radius dω (as angle, not length)
and for corresponding perpendicular radius dφ we respectively have: dω = dφ / (1 - cos(φ))
ω and dω, as angles, are identical on both figures, therefore: dα / sin(α) =
dφ / (1 - cos(φ))
by integration
and solving for φ we get above result
values for α: 0 to π, resulting values for φ: 0 to 2·π
approximations to both limits are highly asymptotic
and absolute symmetrical from both sides of center *
to get φ < 4° on horn torus, α has to be < 10^(-10)°,
to get φ < 3° on horn torus, α has to be < 10^(-14)°,
to get closer than 2° - my computer's capacity fails! (α < 10^(-26))
an extremly slow approach to the horn torus center
reminds me of conditions at the edge of black holes
and of the different views ahead and backwards, when riding a photon - with speed of light: ![]() ]
]
• even slower 'approach' when mapping direct from the complex plane (α = 2·arccot(|z|))
• latter inserted into above formula we eventually get: φ = 2·arccot(-ln|tan(arccot(|z|))|)
• inverse mapping from horn torus to complex plane: |z| = cot(π/2 - arccot(e^(-cot(φ/2))))
• inverse mapping from horn torus back to Riemann sphere: α = π - 2·arccot(e^(-cot(φ/2)))
• most likely no stereographic projection possible, but mathematicians surely will look for!
• non-conformality creates pattern in the
dynamic model, but conformality has a
meaning
* we obtain much simpler formulas when we determine angle α to be
zero at south pole 0
my rough cross-checks with various angles α and differentials
Δω indicate exact validity, but
analytical evidence and search for a projective geometry
I gladly surrender to professionals ...
home
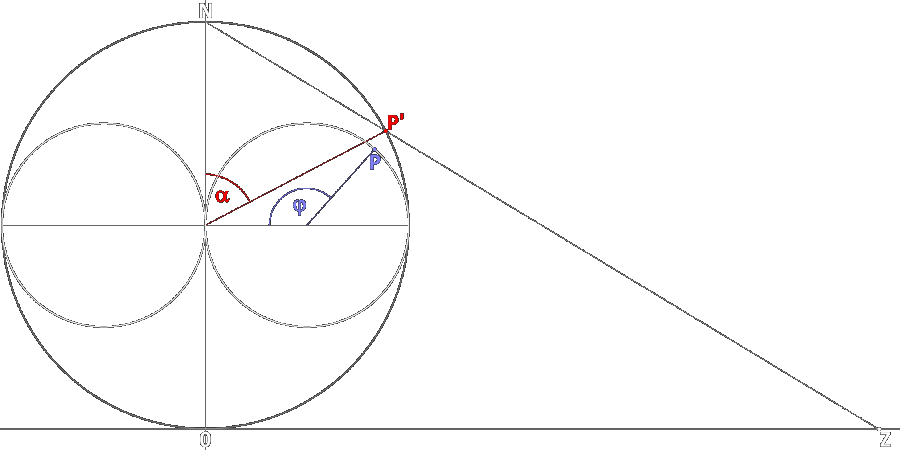
![]() Riemann sphere: 0N = 1 , |z| = 0Z ,
∠0ZN = ∠N0P' = α/2
Riemann sphere: 0N = 1 , |z| = 0Z ,
∠0ZN = ∠N0P' = α/2